What is Compound Interest?

 

Compound interest is one of the most powerful financial tools available to you as a saver and investor. It allows your money to grow over time exponentially; in fact, it’s how many long-term investors grow seemingly small amounts of money into million-dollar nest eggs over time.

In this article, we’ll take a look at what compound interest is, how it works, and how you can use it to your advantage.

What is compound interest?

Compound interest refers to interest that is paid on your principal balance and on any interest you’ve previously earned. When you’re compounding your returns, you’re adding the interest you earn to your balance, and therefore next time interest is calculated, it will be on a larger sum of money.

Consider this simplified example. Let’s say that you put $1,000 into a 3-year CD that pays 5% interest annually. You choose to have all of your interest payments added to the principal, setting yourself up to earn compound interest.

After the first year, the bank pays you $50, which is 5% of $1,000.

Now your balance is $1,050. When your second interest payment is calculated, it will be 5% of this amount, or $52.50. You now have $1,102.50 in the CD. Finally, when the third interest payment is calculated, you’ll receive 5% of this new balance, or $55.13. After compounding your money in a CD for three years, you’ll have a total of $1,157.63.

Notice that the dollar amount of interest you get increases every year. That’s one of the most important concepts to understand about compound interest. With compound interest, time is your best friend.

Compounding frequency

In the real world, most CDs, savings accounts, and other compounding vehicles don’t just pay you once a year. Instead, they use a specific compounding frequency. Your bank accounts likely compound your interest monthly or daily, but quarterly or even continuous compounding aren’t unheard-of.

Here’s how it works. If your bank compounds interest monthly, this means that it will be calculated 12 times per year. So, the bank will divide your interest rate by 12. In the previous example, your 5% interest rate on a CD would become about 0.417%.

So, after one month, this rate would be applied to your $1,000 principal, giving you $1,004.17. In the second month, it would be applied to this new amount, giving you $1,008.35. And so on.

You don’t need to know too much about the mathematics of compounding. And in practice, compounding frequency generally doesn’t make a huge difference. But the more frequent the compounding, the faster your money will grow.

As an example, $1,000 compounded quarterly at 5% for 10 years would grow to $1,643.62. The same amount of money at the same interest rate compounded monthly would grow to $1,647.01. So, monthly compounding would result in an additional $3.39 after 10 years. It’s a difference, but compounding frequency alone generally isn’t a good reason for picking one bank over another.

Compound interest vs. simple interest

There are two basic ways interest can be calculated, simple interest and compound interest.

Simple interest refers to interest that is paid on the principal only. For example, let’s say that you put $1,000 into a savings account that pays 3% simple interest, compounded annually. After one year, the bank would pay you 3% of your balance, or $30. After the second year, you’d get another $30, and so on.

Fortunately, savings accounts in the real world pay compound interest. Continuing our example, you’d be paid $30 for the first year. However, with compound interest your second-year payment would be calculated as 3% of $1,030, which would be $30.90 and would be added to your balance. The next year’s payment would be calculated as 3% of $1,060.90, and so on.

Although savings accounts pay compound interest, it’s still important to understand both types. Treasury bonds are a good example of a real-world investment that pays simple interest. If you buy a $1,000 Treasury bond that pays 5% interest in semi-annual installments, you’ll simply get a payment of $25 twice a year until the bond reaches maturity.

How to calculate compound interest

First of all, you’re likely never going to have to manually calculate compound interest. If you put money into a CD or a savings account, this will be done for you automatically. However, if you’re someone who likes knowing how things work, we’ve got you covered.

There is a formula that you can use to calculate compound interest. You need to know the interest rate, how often interest is being compounded, and the length of time. The formula for compound interest looks like this:

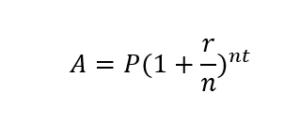
Here’s what it all means:

•         P = Principal, or the initial amount of money you’re starting with
•         r = rate, the interest rate of the investment, expressed as a decimal
•         t = time period of total compounding, in years
•         n = number of times per year interest is compounded
•         A == final amount of money after compounding is done

How compound interest works in the real world

Let’s look at an example. We’ll say that you deposit $1,000 into a 5-year CD that pays 5% interest compounded monthly. So, in this example:

•         P is $1,000
•         r is 0.05 (5% as a decimal)
•         n is 12 (monthly compounding)
•         t is 5 years

Here’s how it would look in the formula:

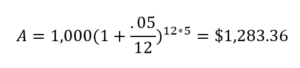
Plugging this into a calculator shows that after five years, your CD would have grown to $1,283.36.

Why understanding compound interest is so important

Compound interest is what drives the returns in your 401(k) or other investments, and can allow your savings to get much larger over long periods of time. Compounding has produced many millionaires (and billionaires) and has helped people learn how to make their money work for them. It is one of the most important concepts that can set you up for long-term financial success.